Vào năm 1982, kỳ thi SAT, một trong những kỳ thi chuẩn hóa đầu vào đại học quan trọng nhất nước Mỹ, đã "gây bão" với một câu hỏi tưởng chừng đơn giản nhưng lại khiến hàng trăm nghìn thí sinh hoang mang tột độ. Cụ thể, trong số 300.000 người dự thi, chỉ có đúng 3 người chọn được đáp án chính xác. Tỷ lệ này là… 0,001% – gần như bằng không.
Và cho đến giờ, dù đã hơn 40 năm trôi qua, đề bài đó vẫn thường xuyên được nhắc lại như một ví dụ điển hình về sự đánh đố thông minh của toán học. Và đây là nội dung của bài toán hình học khiến bao bộ não phải "đứng hình":
Bán kính hình tròn B gấp 3 lần bán kính hình tròn A. Nếu hình A lăn xung quanh hình B, nó phải thực hiện bao nhiêu vòng quay để trở lại điểm xuất phát?
(a) 3/2
(b) 3
(c) 6
(d) 9/2
(e) 9
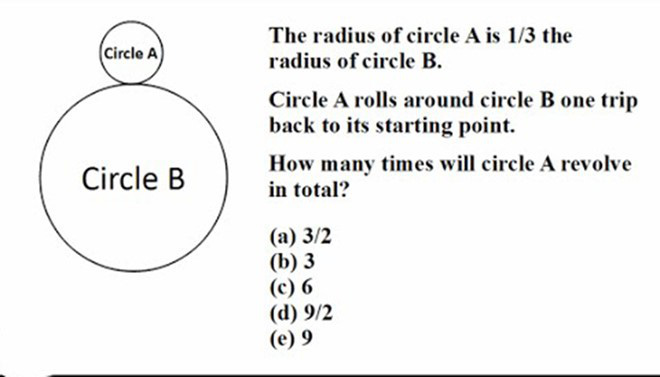
Bài toán hack não chỉ 0,001% người giải đúng.
Trước yêu câu này, không chỉ phần lớn các thí sinh trong kỳ thi năm ấy chọn đáp án (b) mà nhiều người hứng thú với toán học cũng đưa ra lựa chọn tương tự, với lý luận rằng chu vi hình tròn B gấp 3 lần hình A, vậy nên hình A chỉ cần quay đúng 3 vòng để đi hết chu vi hình B.
Thế nhưng lời giải chính xác lại khiến nhiều người "ngã ngửa". Để giải được bài toán này, bạn phải để ý đến một chi tiết quan trọng nhưng lại dễ bị bỏ qua: khi hình A lăn quanh hình B, không chỉ di chuyển theo chu vi mà còn phải "tự xoay" quanh trục của chính nó. Lý do theo tờ The Washington Post đưa ra là vì trong đề có sử dụng từ "revolve". Điều này làm phát sinh thêm một vòng quay nữa mà nhiều người không để ý. Đây là điểm mấu chốt khiến phần lớn thí sinh bị "hớ". Như vậy, đáp án đúng phải là... 4 vòng, và cả năm đáp án đề bài đưa ra đều sai.
Cách giải tham khảo của bài toán này như sau:
Cách 1: Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A. Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A). Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Cách 2: Dễ thấy chu vi hình B gấp 3 lần chu vi hình A. Chia đường tròn lớn thành 3 phần bằng nhau bởi 3 điểm gọi là M, N, P, mỗi phần như vậy có độ dài bằng chu vi hình A. Khi hình A lăn từ M đến N theo chiều kim đồng hồ, bán kính nối tâm hình tròn A với điểm tiếp xúc giữa 2 hình tròn quét một góc 3600 + 1200.. Tương tự cho 2 phần còn lại, để hình A trở về điểm xuất phát thì bán kính hình tròn quét 1 góc tổng cộng là 3 x (3600 + 1200) = 4 x 3600, tức 4 vòng quay.

























